Source: mutiaoctivianti.wordpress.com
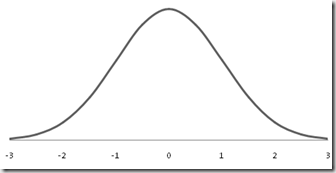
Bentuk kurva normal adalah simetris sehingga luas rata-rata mean ke kanan dan ke kiri masing-masing mendekati 50.
Source: statistikapaitu.blogspot.com
Untuk keperluan pengujian kita harus menghitung frekuensi teoritik E1 dan mengetahui frekuensi nyata atau hasil.
Source: www.semestapsikometrika.com
3 Distribusi Normal Fungsi padat peubak acak normal X dengan rataan π dan variansi π ialah 1 x 2 1 n x.
Source: www.slideshare.net
Standarisasi ini penting dilakukan karena variabel random mempunyai satuan yang berbeda-beda misalnya cm kg tahun dsbAgar dari kurva normal umum dapat ditentukan probabilitas suatu peristiwa maka kurva normal umum ditranformasikan ke kurva normal.
Source: statistikapaitu.blogspot.com
Kurva normal adalah kurva yang memiliki nilai sedang lebih banyak daripada nilai yang kurang atau nilai yang lebih.
Source: www.slideshare.net
Karena luas seluruh di bawah kurva normal adalah 100 maka luas dari titik 222 ke kanan kurva adalah 100 98679 1321 arsir warna hitam pada gambar.
Source: hatta2stat.wordpress.com
Merupakan suatu poligon yang dilicinkan yang mana ordinat sumbu tegak merupakan frekuensi dan absisnya sumbu alas memuat nilai variabel.
Source: www.pngwing.com
Dan e 271828 Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut x 2 1 1 f x e 2 2 Keterangan.
Source: quipper.co.id
Pada kurva B Ο besar maka puncaknya rendah begitu sebaliknya Dua kurva simetris Dua kurva simetrisUntuk membentuk satu kurva sebagai standar yaitu kurva normal standardapat dilakukan dengan melakukan transformasi terhadap rumus Z.
Source: www.rumusstatistik.com
Untuk tiap pasang Β΅ dan Ο sifat -sifat di atas selalu kurva normal dengan ΞΌ 10 danΟ 5 kurva normal dengan ΞΌ 20 dan.
Source: zbook.org
Distribusi normal sangat sesuai dengan distribusi empiris sehingga dapat dikatakan bahwa semua kejadian alami akan membentuk distribusi ini.
Source: belajarkalkulus.com
Kurva normal adalah kurva yang memiliki nilai sedang lebih banyak daripada nilai yang kurang atau nilai yang lebih.
Source: docplayer.info
Kurva normal ialah kurva yang simetris yang berarti bahwa kurva ini akan membagi luas kurva menjadi 2 belahan yang samaSeluruh luas kurva 1 atau 100 dan rata-rata Β΅ membagi luas kurva menjadi 2 belahan yang samaBerarti luas tiap belahan ialah 50.
Source: slideplayer.info
Angka ini menunjukkan bahwa luas di bawah kurva normal baku dari titik 222 ke kiri kurva adalah sebesar 98679.
Source: yuvalianda.com
Bentuk Kurva Normal.
Source: tambahpinter.com
Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss.
Source: nuryantostiess.blogspot.com
Pada kurva B Ο besar maka puncaknya rendah begitu sebaliknya Dua kurva simetris Dua kurva simetrisUntuk membentuk satu kurva sebagai standar yaitu kurva normal standardapat dilakukan dengan melakukan transformasi terhadap rumus Z.
Source: mutiaoctivianti.wordpress.com
Kurva normal merupakan suatu poligon yang dilicinkan yang mana ordinatnya memuat frekuensi dan absisnya memuat nilai variabel.
Source: ichi.pro
Bentuk Kurva Normal.
Source: www.rumusstatistik.com
Distribusi normal sangat sesuai dengan distribusi empiris sehingga dapat dikatakan bahwa semua kejadian alami akan membentuk distribusi ini.
Source: www.rumusstatistik.com
Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss.
Source: www.rumusstatistik.com
M y 4x 3 - 14 x 42 3 - 142 32 - 28 4 gradien m 4 melalui A 28 Jadi persamaan garis singgungnya adalah.
Source: www.slideshare.net
Kurva normal merupakan suatu poligon yang dilicinkan yang mana ordinatnya memuat frekuensi dan absisnya memuat nilai variabel.
Source: www.youtube.com
Kurva normal ialah kurva yang simetris yang berarti bahwa kurva ini akan membagi luas kurva menjadi 2 belahan yang samaSeluruh luas kurva 1 atau 100 dan rata-rata Β΅ membagi luas kurva menjadi 2 belahan yang samaBerarti luas tiap belahan ialah 50.
Source:
Dan e 271828 Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut x 2 1 1 f x e 2 2 Keterangan.
Source: slideplayer.info
Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss.
Source: www.rumusstatistik.com
Pada kurva B Ο besar maka puncaknya rendah begitu sebaliknya Dua kurva simetris Dua kurva simetrisUntuk membentuk satu kurva sebagai standar yaitu kurva normal standardapat dilakukan dengan melakukan transformasi terhadap rumus Z.
Source: slideplayer.info
Ο 31416 e 27183 Β΅ rata-rata Ο simpangan baku Begitu π dan π diketahui maka seluruh kurva normal diketahui.
Source: slideplayer.info
Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss.
Source: www.youtube.com
Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss.
